Vortrag Ralf Lempken bei der Deutschen Gesellschaft für Chronometrie in Trier

Folie 1: Können Kalender falsch gehen ?

Jeder, der eine Armbanduhr besitzt, hat sich evtl. schon mal Gedanken über deren Ganggenauigkeit gemacht, und dabei festgestellt haben, dass für eine gesicherte Aussage dazu ein Vergleichsmaßstab erforderlich ist. Heute kann jeder, der nicht alleine auf einer einsamen Insel lebt seine evtl. noch alte mechanische Armbanduhr mit funkgesteuerten Quarzuhren oder der Uhr seines Smartphones synchronisieren.

Uhren messen den Ablauf der Zeit auf Zeitskalen bis zu einem (Sonnen)-Tag. Kalender sind ebenso Zeitmesser deren Zeitskala aber erst bei einem (Sonnen)-Tag beginnt. Während Uhren zyklisch mit jedem Tag, ohne Unterscheidungsmöglichkeit, wieder bei 0 beginnen. Die Zeit läuft dabei praktisch ohne Anfang und Ende im Kreis.

Beim Kalender dagegen, sind die Zeitzyklen (Jahre) entlang einer Geraden ohne Anfang und Ende abgewickelt. Dies macht eine Unterscheidung der einzelnen Abschnitte möglich. Bei jedem Instrument, dessen zu zählende Basiseinheit schwanken kann, ist die Frage nach der Ganggenauigkeit berechtigt. Wie bei der Uhr, so auch beim Kalender.

(Einige Folien des Vortrages sind in dieser Präsentation ausgelassen.)

Folie 3 Überlegungen zu Prinzip und Ganggenauigkeit von Kalendern

Die ersten beiden Punke habe ich schon in meinem einleitenden Vergleich zwischen Uhr und Kalender kurz erläutert.
Der dritte Punkt bedarf noch einer Erläuterung.

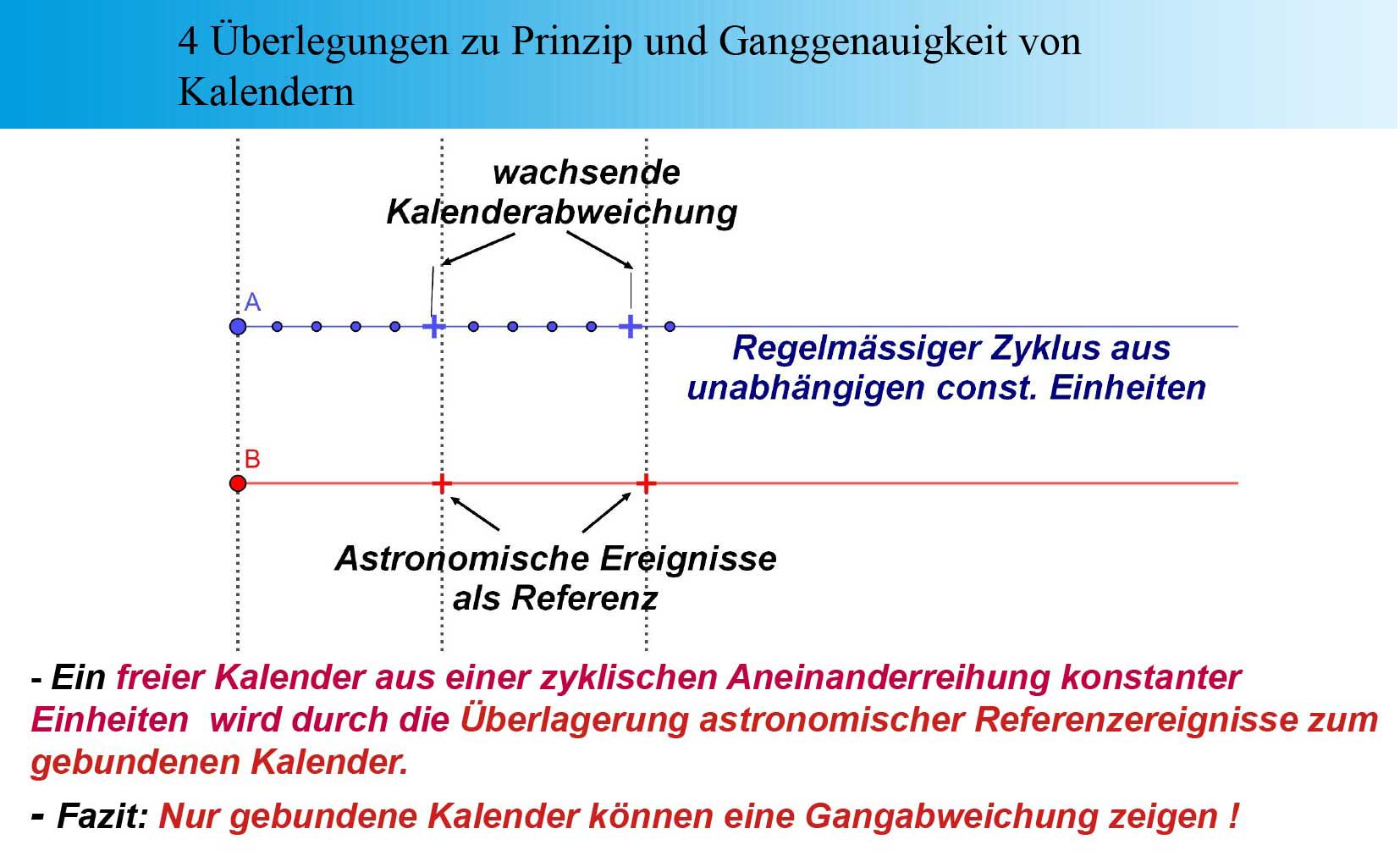Folie 4: Überlegungen zu Prinzip und Genauigkeit von Kalendern

Der blaue Zeitstrahl repräsentiert einen zyklischen, ungebundenen Kalender.
Der rote Zeitstrahl definiert eine duch unabhängige, in absolut konstanten Zeitabständen auftredende Ereignisse gebildete Zeitbasis.

Ein gutes Beispiel dafür ist der alte ägyptische Sonnen-Kalender mit seinem festen 365-Tage Jahr. Dieser Kalender ist der theoretische Vorläufer des julianischen-, bzw. Gregorianischen Kalenders. Die konstante Zeitbasis ist darin das jährlich wiederkehrende erstmalige Erscheinen des hellen Sterns Sirius kurz vor Sonnenaufgang in der Morgendämmerung (“heliakischer Aufgang”).

Dieser Aufgang eilt dem Kalender jährlich um 6 Stunden voraus, und “läuft” somit in 4x365+1=1461 äg. Jahren durch alle Monate des äg. Kalenders. Nach dieser “Sothis-Periode” ist der Sirius-Aufgang wieder mit dem Kalender synchron.
Dies macht vom Prinzip her eine Kalenderschaltung überflüssig.

Folie 5: Die Wandsonnenuhr von Gerhard Benna

Dies ist ein Beispiel, wie sich die Synchronisation zwischen einem Kalender und dessen astronomische Fixpunke mittels einer Sonnenuhr überprüfen lässt.

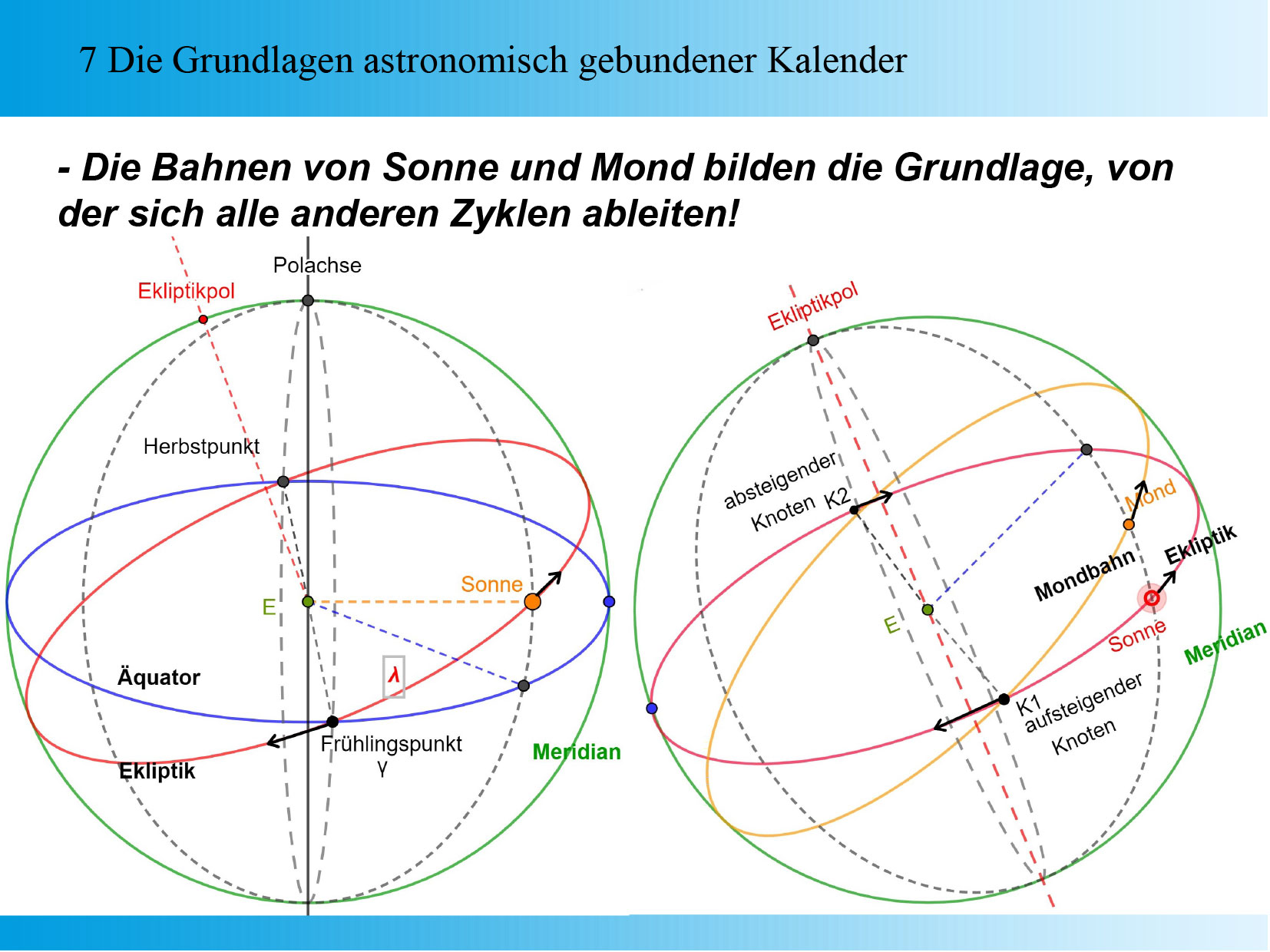Folie 7: Die Grundlagen astronomisch gebundener Kalender

Hier nun ein wenig astronomisches Grundlagenwissen. Entscheidend für unseren an den Frühlingspunkt gebundenen gregorianischen Kalender sind die beiden Schnittpunkt-Paare

a) (linkes Bild) zwischen der Äquatorebene (blau), und der scheinbaren Sonnenbahn (Ekliptik, rot), sowie
b) (rechtes Bild) zwischen der Ekliptik (rot), und der scheinbaren Bahn des Mondes (orange) – die Mondknoten.

Der Frühlingspunkt ist der (wandernde!!!) Nullpunkt der ekliptikalen Winkelteilung am Himmel.
Die Beobachtung der Positionen von Sonne und Mond relativ zu diesen beiden Schnittpunktpaaren, sowie relativ zum Sternenhimmel ist das entscheidende Kontrollinstrument zur Beurteilung der Ganggenauigkeit unseres Kalenders.

Text zu 8: Astronomische Zyklen als Referenz für gebundene Kalender

Zur Kontrolle des Kalenders sind im Prinzip (fast!) nur 4 verschiedene astronomische Beobachtungen erforderlich, welche Lauf und Position von Sonne und Mond entlang ihrer scheinbaren Bahnen betreffen. Die Genauigkeit der Ergebnisse hängt wesentlich von den Beobachtungszeiträumen ab. Je länger desto besser. Deshalb ist man hier auf überlieferte historische Finsternisbeobachtungen angewiesen.

An dieser Stelle muss auf eine Einschränkung bezüglich der Beobachtungsmöglichkeiten hingewiesen werden. Das sogen. Platonische- oder Weltenjahr (a-pla), als Zeit eines vollständigen Durchlaufs des Himmelspols durch den (gedachten) Präzessionskreis am Sternenhimmel.
Wegen der Größenordnung von 30000 +/- X Jahren sind auch Teile dieses Umlaufs in einem Menschenalter nicht mit ausreichender Genauigkeit beobachtbar. Hier greift man auf historisch überlieferte Positionsmessungen von Sternen mit verschwindender Eigenbewegung zurück, um daraus die relative Positionsänderung bezogen auf die heutige Zeit zu berechnen.

Erstaunlich genaue Positionsmessungen wurden in der Antike vor allem von dem griech. Astronomen Hipparch durchgeführt. Seine ältesten überlieferten Beobachtungen stammen aus dem Jahr 721 BC. Von diesen Beobachtungen aus bis heute haben sich die Sternpositionen präzessionsbedingt bereits um etwa 30 Grad geändert (1 Grad pro 90 bis 100 Jahre). Die aus den Beobachtungen berechneten Größen - drakonitischer Monat (m-drak) und - Finsternisjahr (T-Fi) sind vor allem bei der Synchronisation von Kalendern verschiedener Epochen wichtig.

9 - entfällt

Text zu 10: Die Beziehung zwischen astronomischem und bürgerlichem Kalender

Zwei weitere, die Ganggenauigkeit möglicherweise beeinflussende Faktoren kommen beim Übergang vom (theoretischen) astronomischen Kalender zum bürgerlichen Kalender hinzu.

Das sind:
1. die zur Synchronisation mit den Beobachtungen eingefügten Schalteinheiten, und
2. die zur Synchronisation der über Jahrtausende wechselnden Kalenderepochen.
Durch falsch überlieferte Kalenderepochen können Sprünge oder Überlappungen im kontinuierlichen Zeitfluss auftreten. Ein möglicher systematischer Fehler ist die begrenzte Genauigkeit der Angleichung an den astronomischen Zyklus durch die Schalteinheiten. Ein möglicher Lösungsansatz für das Problem der Kalenderepochen ist die Julianische Tageszählung.

Text zu 11: Die Julianische Tageszählung als „größter gemeinsamer Teiler“ in der Chronologie

Was der grösste gemeinsame Teiler in der Mathematik, das ist die Julianische Tageszählung in der Chronologie !

Die Epoche ist so gewählt, dass Sonnen- und Mondzirkel (28 bzw. 19 trop. Jahre) jeweils auf 1 stehen. Zusätzlich steht an diesem Tag auch der 15-jährige Zyklus der Indiktion (Römerzinszahl) auf 1. Diese Kombination kann sich erst nach 25x19x15=7980 Jahren wiederholen.

Folie 12: Die Julianische Tageszählung als „größter gemeinsamer Teiler“ in der Chronologie

Was der grösste gemeinsame Teiler in der Mathematik, das ist die Julianische Tageszählung in der Chronologie !

Die Epoche ist so gewählt, dass Sonnen- und Mondzirkel (28 bzw. 19 trop. Jahre) jeweils auf 1 stehen. Zusätzlich steht an diesem Tag auch der 15-jährige Zyklus der Indiktion (Römerzinszahl) auf 1.

Diese Kombination kann sich erst nach 25x19x15=7980 Jahren wiederholen.

Text zu 13: Die „Benna-Gleichung“ als Verbindung zwischen Kalender und astronomischer Beobachtung

Das Rechenverfahren lässt sich interpretieren als: Abfahren einer Strecke (JD(x)+K) mit einer Messrolle des Umfangs m mit dem Ziel, die Restlänge zu bestimmen, in welcher m nicht mehr vollständig enthalten ist. Mit der nächsten Folie machen wir den Sprung vom allgemeinen auf den speziellen Fall.

Folie 14: Die „Benna-Gleichung“ als Vermittler zwischen wahrer Sonnenposition und Kalenderdatum

Hier wird ein in julianischer Tageszählung (JD) angegebenes Datum mit der siderischen Jahreslänge als Maßstabeinheit vermessen. Jede Einheit des Maßstabes markiert die Position der Sonne vor dem Sternhimmel nach Ablauf eines (siderischen) Jahres. Diese Position ist immer gleich, die Sonne steht an diesen Punkten also immer vor dem gleichen Stern.

Am Start der Messung steht die Sonne vor einem der Schnittpunkte der Ekliptik mit der Äquatorebene (dem Frühlingspunkt).

Bei dieser Messanordnung ist die mit der Gleichung berechnete „Restlänge“ immer gleich dem beobachteten Abstand der Sonne vom nicht beobachtbaren Frühlingspunkt. Diese Restlänge ist die sogenannte „ekliptikale Länge λ der Sonne.

Was verbirgt sich hinter der Konstanten “K”? Hier kommt das Platonische-, oder Weltenjahr Jahr ins Spiel.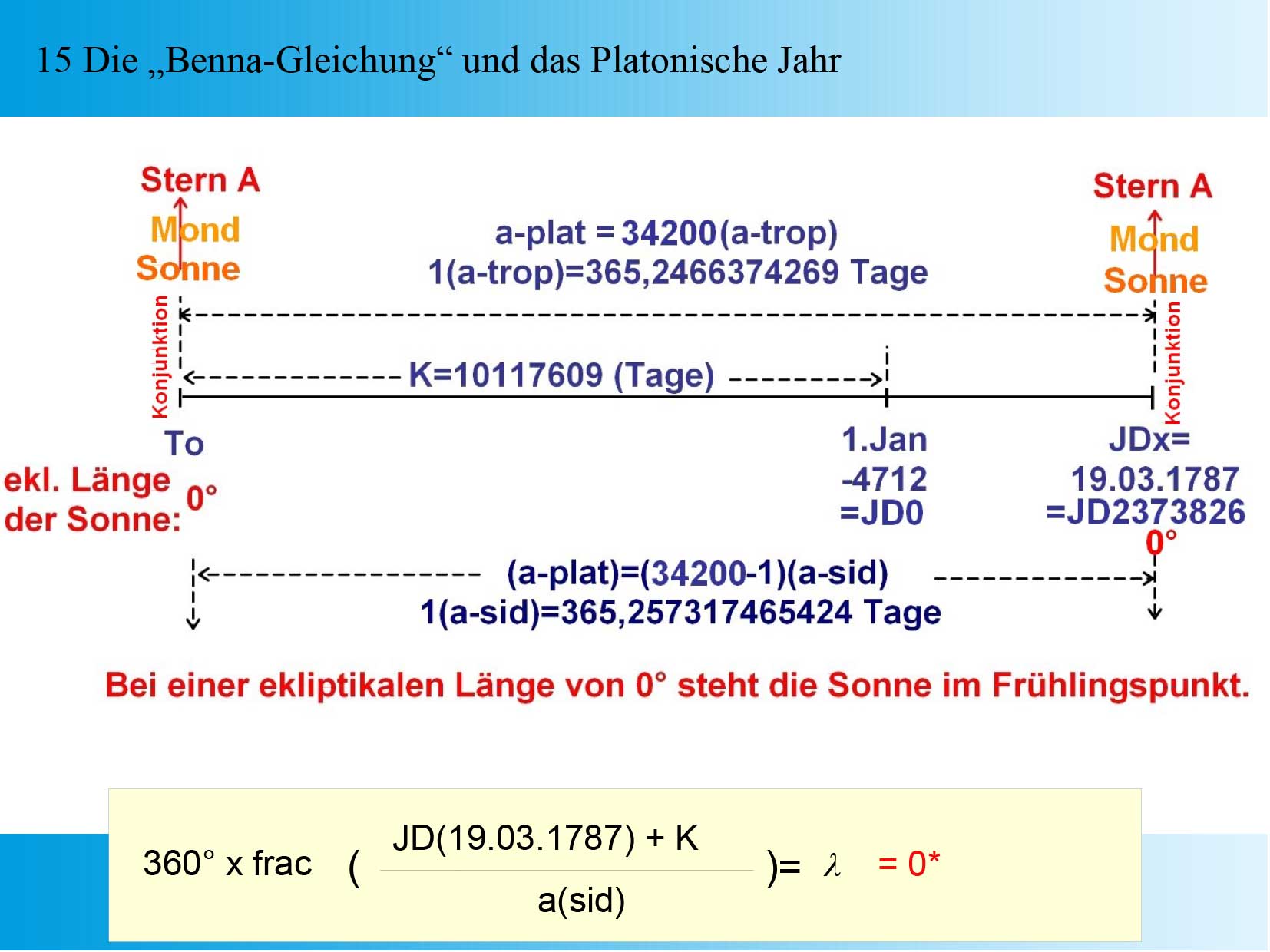

Folie 15: Die “Benna-Gleichung” und das “Platonische Jahr”

Das “Platonische-” oder Weltenjahr, ist der Zeitraum welcher die gedanklich bis an den Sternhimmel verlängerte Erdachse für einen vollständigen Umlauf um den Himmelspol benötigt. Zu Beginn des Platonischen Jahres soll sowohl Frühlingsanfang sein, die Sonne vor einem definierten Stern stehen., als auch eine Sonnenfinsternis stattfinden.

Diese Bedingungen wiederholen sich dann in exakt gleicher Weise am Ende dieses Weltenjahres. In einem Weltenjahr sind per Definition eine ganze Anzahl (N) tropischer Jahre, und genau eine um 1 verminderte Anzahl siderischer Jahre enthalten.

Multipliziert man die von Herrn Benna angegebene Länge des tropischen Jahres mit der Anzahl von 34200 Jahren so ergibt sich bis auf 9 Nachkommastellen die ganze Anzahl 12491435 Sonnentage. Teilt man diese Zahl wiederum durch 34199 siderische Jahre, so erhält man die zugehörige Länge des siderischen Jahres.

Es ergibt sich so ein System, dessen 3 Parameter durch deren gegenseitige Abhängigkeit exakt abgestimmt werden kann. Die Konstante K ergänzt die Julianische Tages-Nr des 19.03.1787 auf die Anzahl der Sonnentage in einem Weltenjahr von 34200 tropischen Jahren.

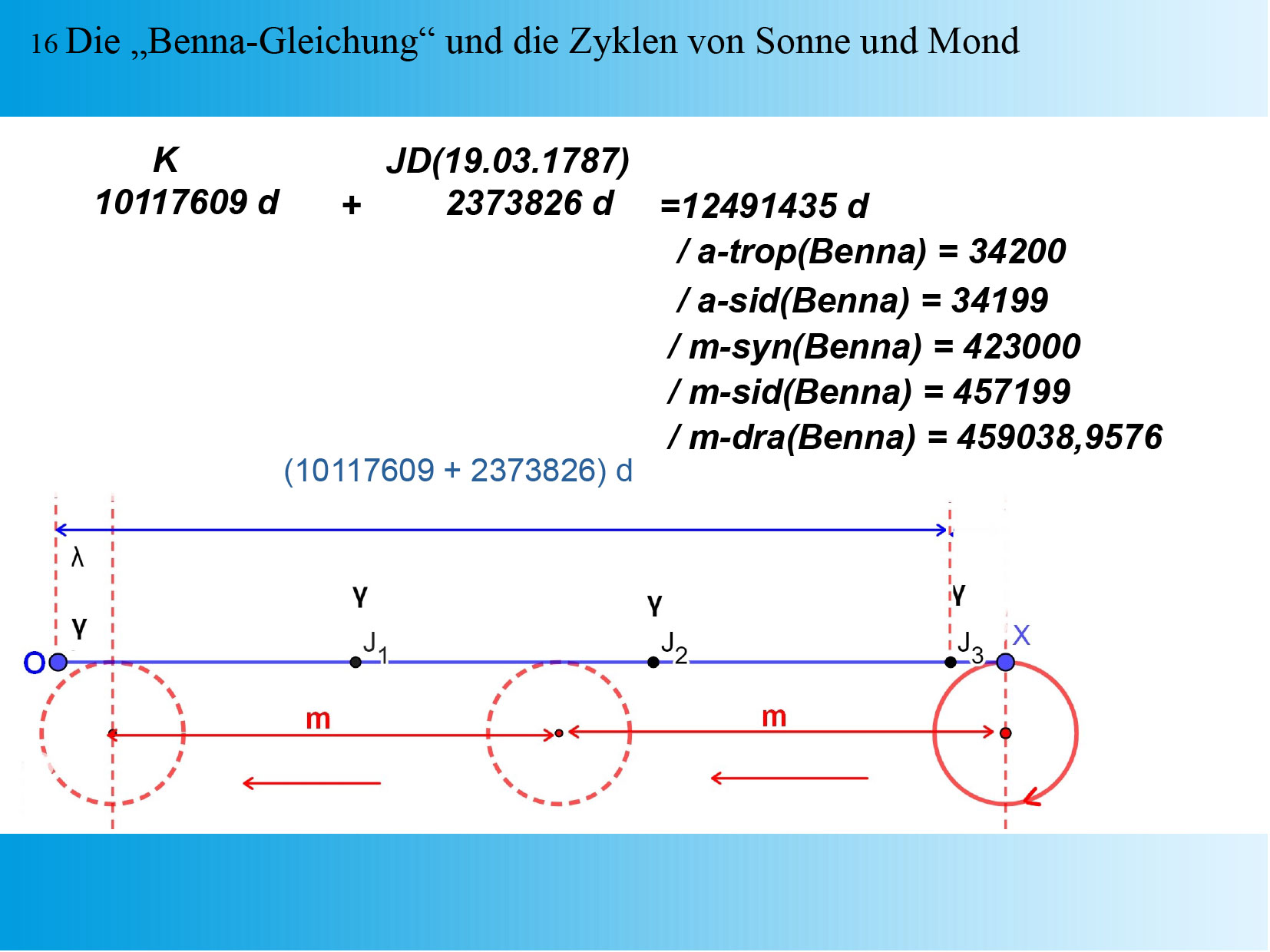Folie 16: Die “Benna-Gleichung” und die Zyklen von Sonne und Mond

Die “Benna-Gleichung” transformiert die Epoche der Julianischen Tageszählung auf den Beginn des Platonischen Jahres, welches am 19.03.1787 endet. Definitionsgemäss sin in diesem Zeitraum eine ganze Anzahl tropischer Jahre, sowie die um 1 verminderte Anzahl siderischer Jahre enthalten.

Wenn an beiden Endpunkten des Zeitraums eine Sonnenfinsternis stattfindet, so müssen auch die Anzahl der darin enthaltenen synodischen und siderischen Monate ganzzahlig sein. Anhand verifizierbarer Angaben zu Sonnen- und Mondfinsternissen können sich die daraus ergebenden Jahres- und Monatslängen überprüft werden.

Hier sind vor allem die uns von Claudius Ptolemäus überlieferten babylonischen, sowie seine eigenen Finsternisbeobachtungen zu nennen.

17 - entfällt

Text zu 18: Konstruktion einer Finsternisuhr

Für das Auftreten einer Finsternis müssen Sonne und Mond in der Nähe eines der beiden Schnittpunkte der Mondbahn mit der Ekliptik stehen. Diese Schnittpunkte sind die beiden um 180° gegeneinander versetzten Mondknoten. Verifizieren lassen sich die historischen Finsternisangaben mit einer “Finsternisuhr”.

Diese ist eine Parallelprojektion der Bahnen von Sonne und Mond in die Ekliptikebene. Während am Himmel entgegen den Bewegungen von Sonne und Mond rückläufig durch die Ekliptik wandern, nehmen sie auf der “Finsternisuhr” feste Positionen ein. Die Sonne macht dabei in einem Finsternisjahr (etwa 346,62 Tage) eine vollständige Linksdrehung. Der Mond benötigt für einen solchen Umlauf nur einen drakonitischen Monat von etwa 27,212 Tagen.

Text zu 19: Vergleich der wissenschaftlichen, mit den von Herrn Benna modifizierten Monats- und Jahreslängen.

Dargestellt ist hier die Konstellation von Sonne und zueinander, sowie deren relativer Position zu den Mondknoten. Für eine in der Literatur (Ginzel Bd.2, S531) angegebene zentrale Sonnenfinsternis am 28.03 0005.

Diese wird hier bezogen auf die Epoche 25.06.-744. An diesem Datum haben die Babylonier lt. den Angaben von Claudius Ptolemäus eine zentrale Sonnenfinsternis beobachtet. Für diese Epoche passt die mit den von der Wissenschaft akzeptierten Werten durchgeführte Berechnung recht gut mit den Finsternisangaben überein (linke Darstellung).

Die Berechnung mit den modifizierten Werten für den drakonitischen Monat und das Finsternisjahr zeigt auf die selbe Epoche bezogen noch keinen gravierenden Unterschied, insofern die “Finsternisuhr” hier auch eine zentrale Finsternis anzeigt (Darstellung rechts).

Wechselt man aber die Richtung der Betrachtung und berechnet die Konstellation für eine historische Finsternis bezogen auf eine im 21. Jahrhundert beobachtete ergeben sich deutlich veränderte Verhältnisse. Dafür soll hier das Datum der am 10.06.2002 beobachteten Sonnenfinsternis als neue Epoche der “Finsternisuhr” gewählt werden.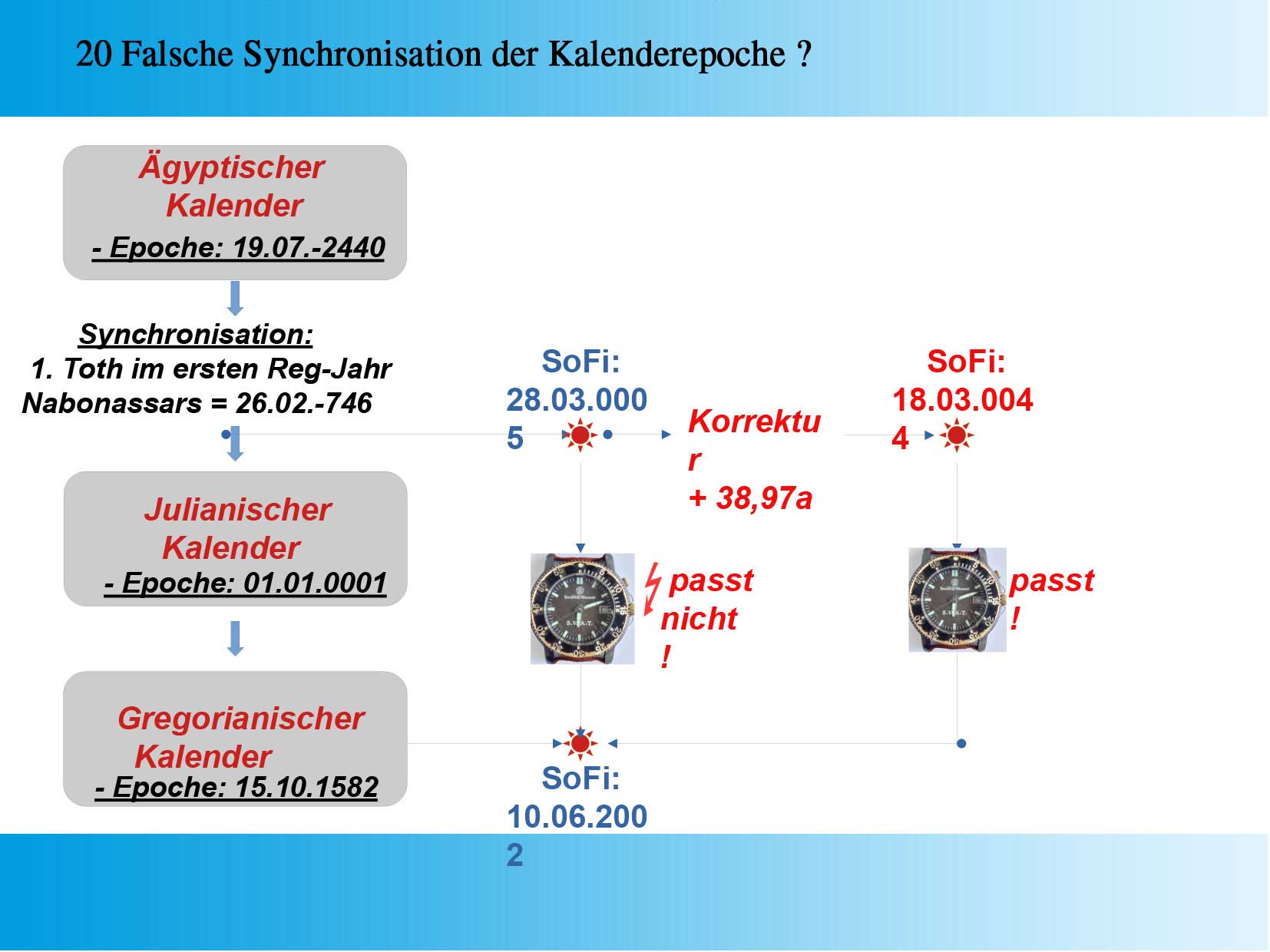

Folie 20: Falsche Synchronisation der Kalenderepoche

Ausgehend von der durch Claudius Ptolemäus durchgeführten Synchronisation des ägyptischen Kalenders auf den Julianischen Kalender, wurde hier zunächst die Epoche der Finsternisuhr auf die Sonnenfinsternis vom 28.03.0005 eingestellt. Berechnet man damit die Positionen von Mond und Sonne für die Sonnenfinsternis vom 10.06.2002, so deuten die Zeiger der Finsternisuhr nicht auf eine Finsternis hin.
Verschiebt man dagegen die Epoche um 14235 Tage = 38,97 Jahre in die Zukunft, so zeigen die Zeiger für Sonne und Mond mit guter Genauigkeit die Konstellation der Finsternis vom 10.06.2002. Dieses Ergebnis ist mit beliebigen anderen Finsternissen der jüngeren Vergangenheit oder auch mit zukünftigen reproduzierbar.

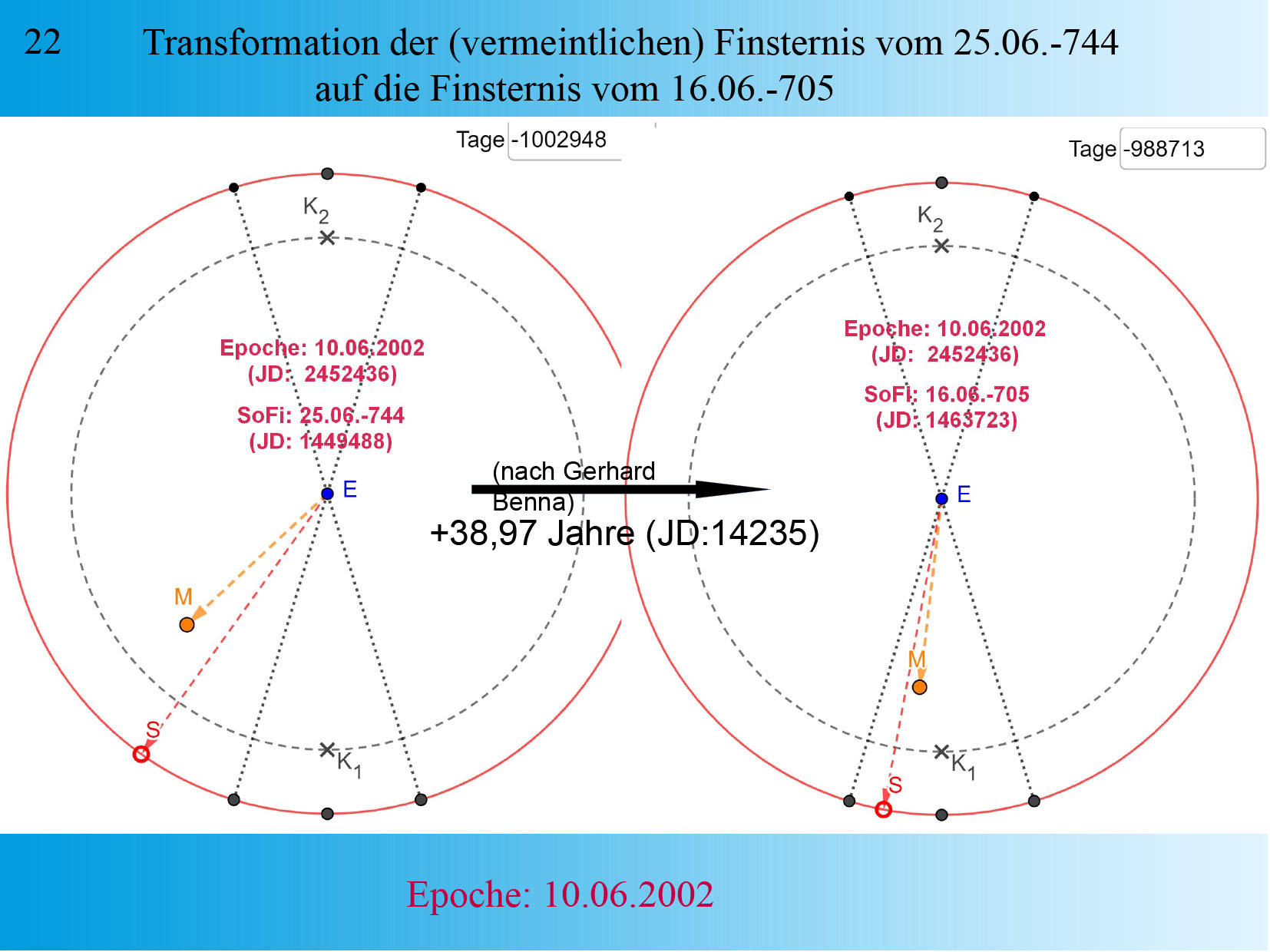
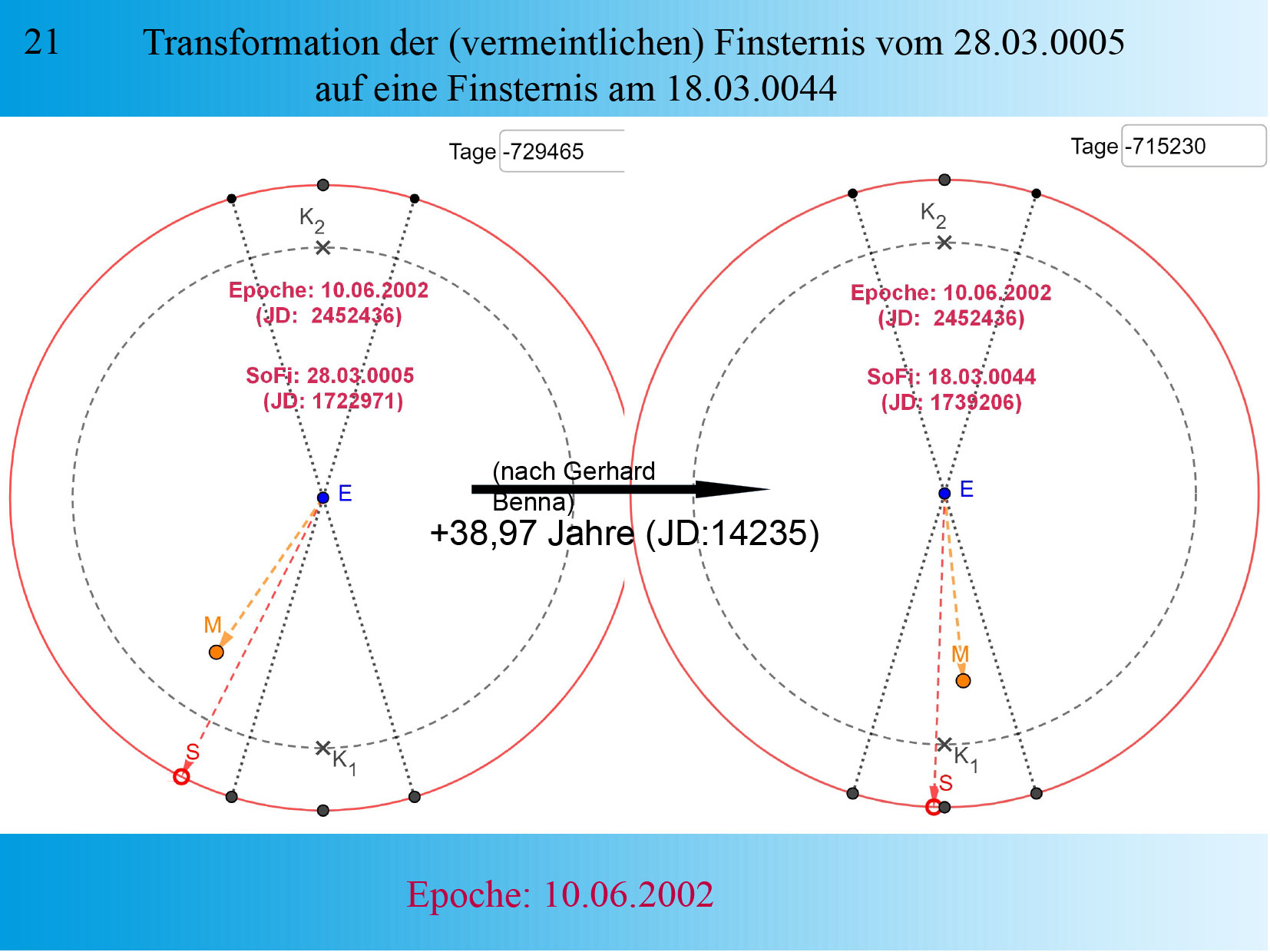Folie 21/22: Transformation der (vermeintlichen) Finsternis vom 28.03.2005 auf eine Finsternis am 18.03.0044.

Dargestellt ist links wieder die Finsternis vom 28.03.0005. Hier aber ist die “Finsternisuhr” auf die Epoche 10.06.2002 eingestellt. Das Datum einer im unteren Mondknoten beobachteten zentralen Sonnenfinsternis. Nach Berechnung mit den modifizierten Konstanten und der neuen Epoche zeigt die “Finsternisuhr” für den 28.03.0005 keine Finsternis mehr an.

Korrigiert man allerdings dieses historische Datum um die von Herrn Benna ermittelten 14235 Tage (=38,97 Jahre) in der Zeit nach vorne auf den 18.03.0044, ergibt sich wieder eine zentrale Sonnenfinsternis. Um dieses Datum herum ist in der wissenschaftlichen Literatur (Ginzel, Bd. 2) erst wieder für den 01.08.0045 eine zentrale Sonnenfinsternis dokumentiert.

Die Wahrscheinlichkeit, dass dieser Korrekturwert kein Zufall ist, steigt mit der Anzahl der historischen Finsternisse, für welche diese “Transformation” die Konstellation für eine Finsternis ergibt. Eine solche Transformation wird notwendig, wenn in dem Zeitraum zwischen den betrachteten Finsternissen eine fehlerhafte Synchronisation zweier Kalendersysteme durchgeführt wurde.

Claudius Ptolemäus stellte im zweiten nachchristlichen Jahrhundert folgende Zuordnung her:
Der 1. Thoth im 1. Regierungsjahr Nabonassars nach dem ägyptischen Kalender sollte dem 26. 02.-746 des julianischen Kalenders entsprechen. Für dieses Datum berechnete Ptolemäus eine Elongation zwischen Sonne und Mond 70° 17’.